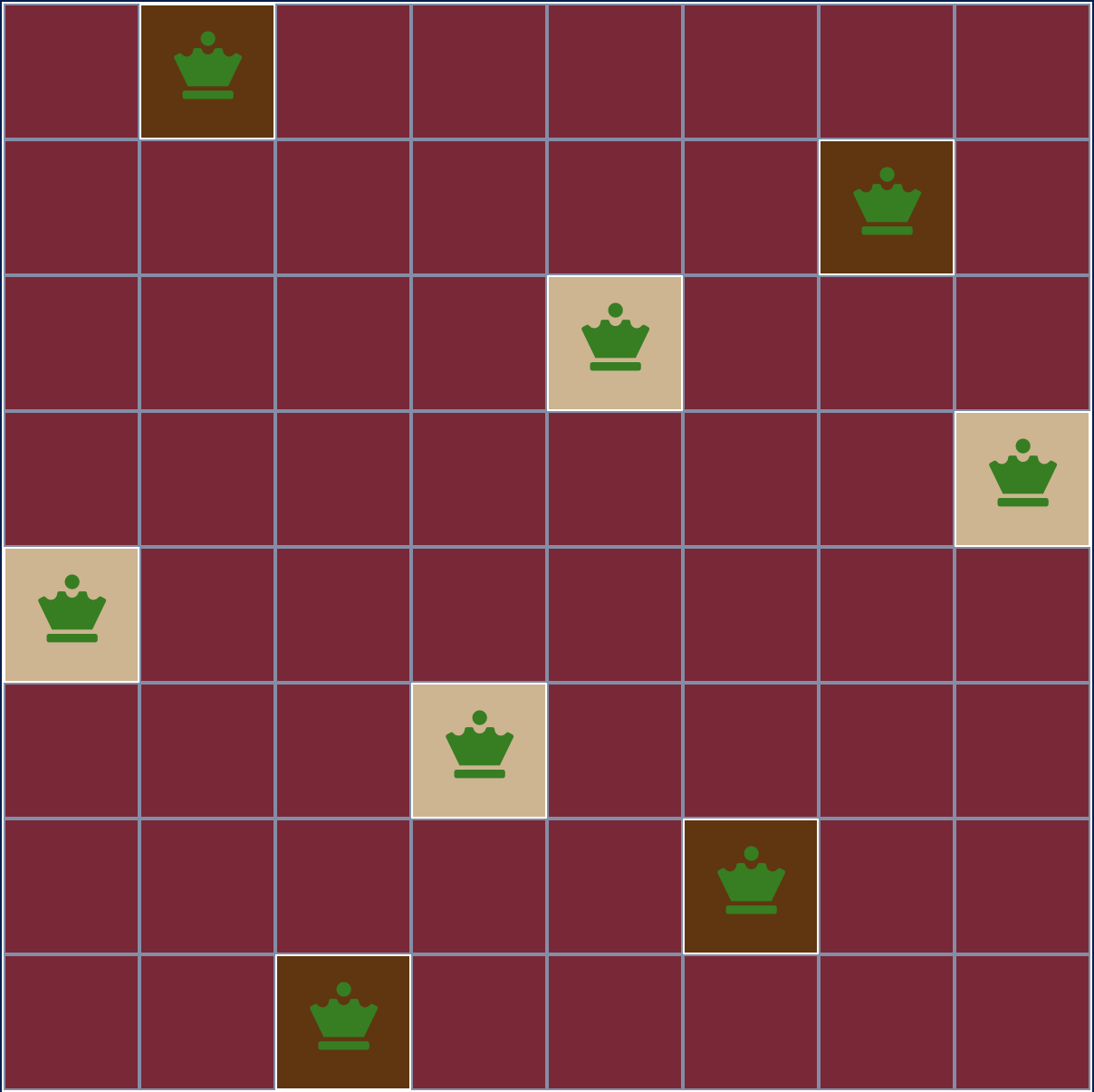
In the N queens puzzle, the goal is to place N queens onto an NxN chess board
such that no two queens are attacking each other.
The N Queens problem asks how many ways there are to place N queens in this way
onto an NxN board. It is a classic exercise in backtracking. In my visualizer,
you may place a queen on any square by clicking, except for squares that are
already attacked by other queens, which will be marked. The number of queens you
have placed will be tracked and displayed. Also, the number of possible solutions,
given the queens you have placed so far, will be calculated using a straightforward
backtracking algorithm and displayed in real time.
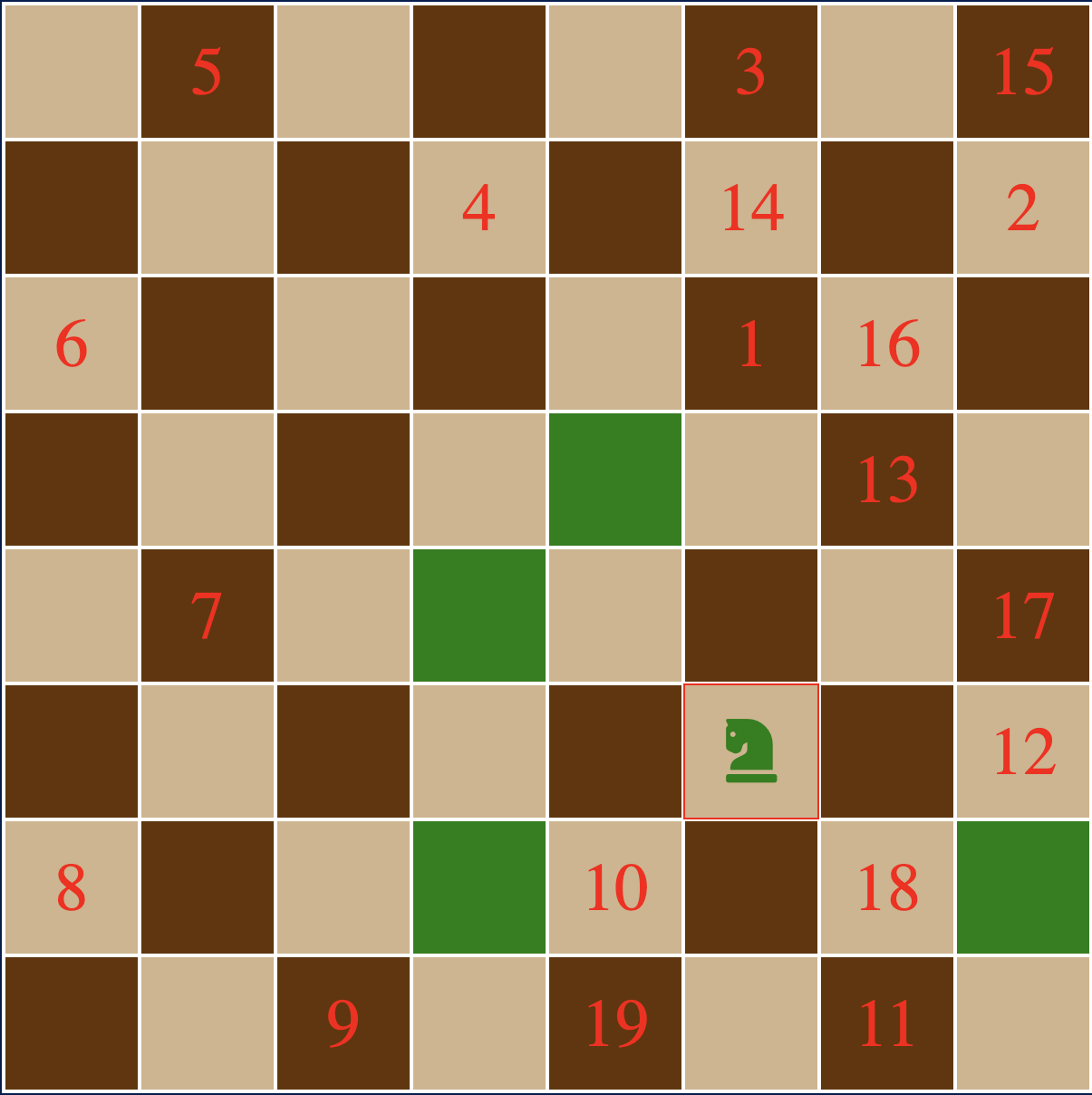
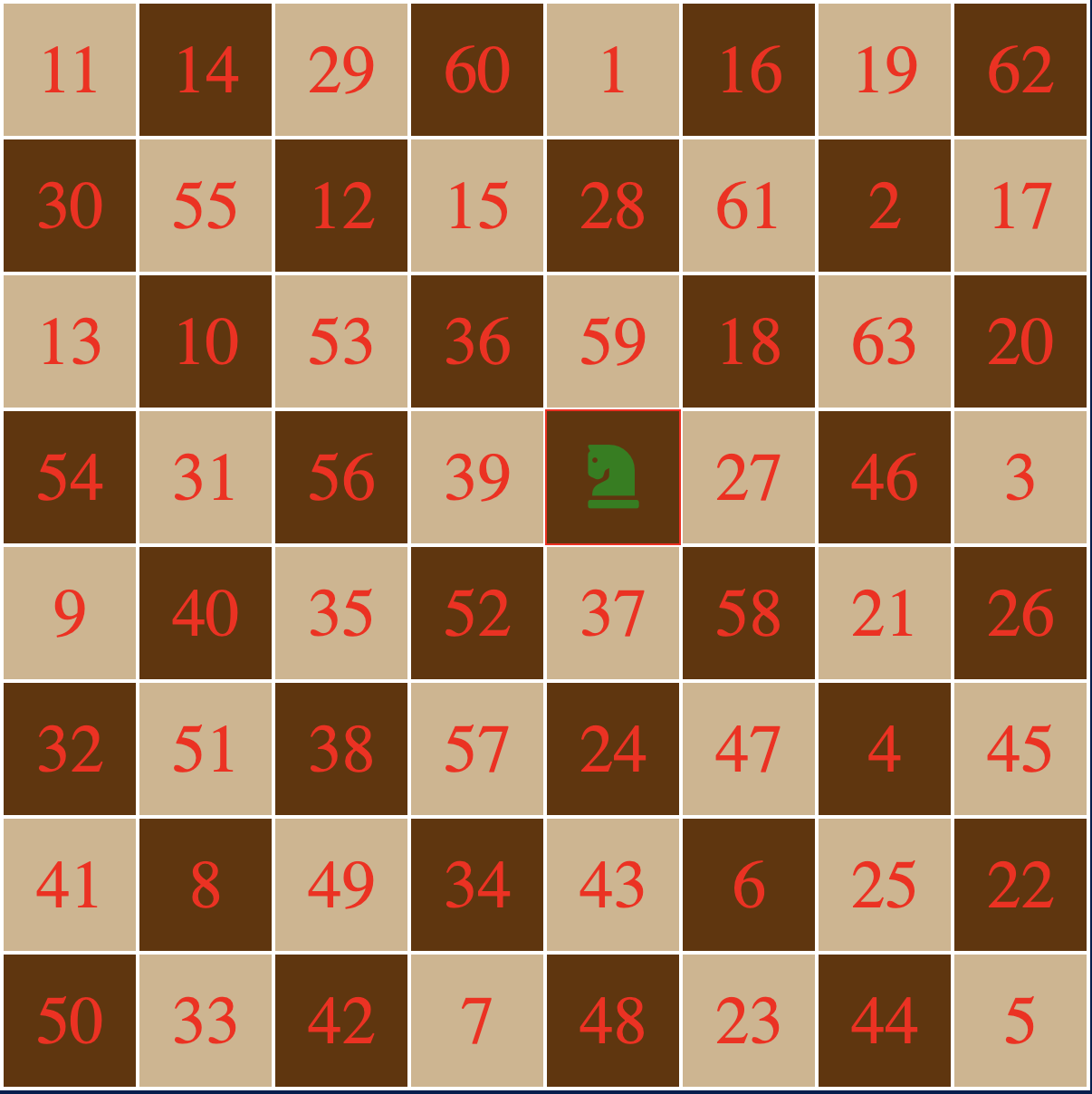
To complete the Knight's Tour puzzle, you must find a way to move a knight
N2 times on an NxN chessboard such that the knight visits all
N2 squares exactly once, that is without missing or revisiting
any square.
You may set the size of the board and then click squares to place and move
knights. Possible next moves will be highlighted. The number of moves you
have taken will be tracked. In addition, my algorithm continually searches
for a complete tour using the Warnsdorff heuristic as you make moves, and
displays whether a complete tour has been found. Because the heuristic is
non-deterministic, this display of whether a complete tour exists may be
wrong at times, i.e. it may incorrectly display "no tour exists" for some
configurations of moves where a tour does in fact exist.